Extensions to the Basic ERGM

Now that we have a general understanding with ERGMs and some familiarity with using them in R, we turn to a conceptual discussion of extensions to ERGMs. The purpose of this discussion is to provide you with a preview of what the basic ERGM can do with two tweaks.

Table of contents

1. Adding Constraints
   1. Bipartite Networks
   2. (Kind of) Directed Acyclic Graphs
2. Specifying Relational Contexts
   1. Multilayer Networks
   2. Temporal Networks

Adding Constraints

Constraints are researcher-specified dyads where observed outcomes are not modelled as outcomes.

• These dyads are held at their observed values, tie or no tie (i.e. constant or treated as exogeneous)
• This removes the tie from being part of the outcome data (i.e. their rows are removed in the data)
• They still matter to local configuration counts/calculation of change statistics

They can be used in a number of ways to account for the data generating process

• In temporally-aggregated network, sometimes actors never existed at the same time
• For example, some states from the post-Cold War network never existed at the same time in the global system
• Constraints can also be used to get rid of “outliers” in the data
• For example, in a scientific lab collaboration network, the lab responsible for producing a widely-used reagent might have their ties fixed at the observed state

More important for the current discussion, constraints can be used systematically to produce specific network types

Bipartite Networks

Bipartite networks have two different types of nodes; ties can form across types but not within types.

• People attending meetings (e.g. policy actors and shared policy forums)
• Legislators signing bills

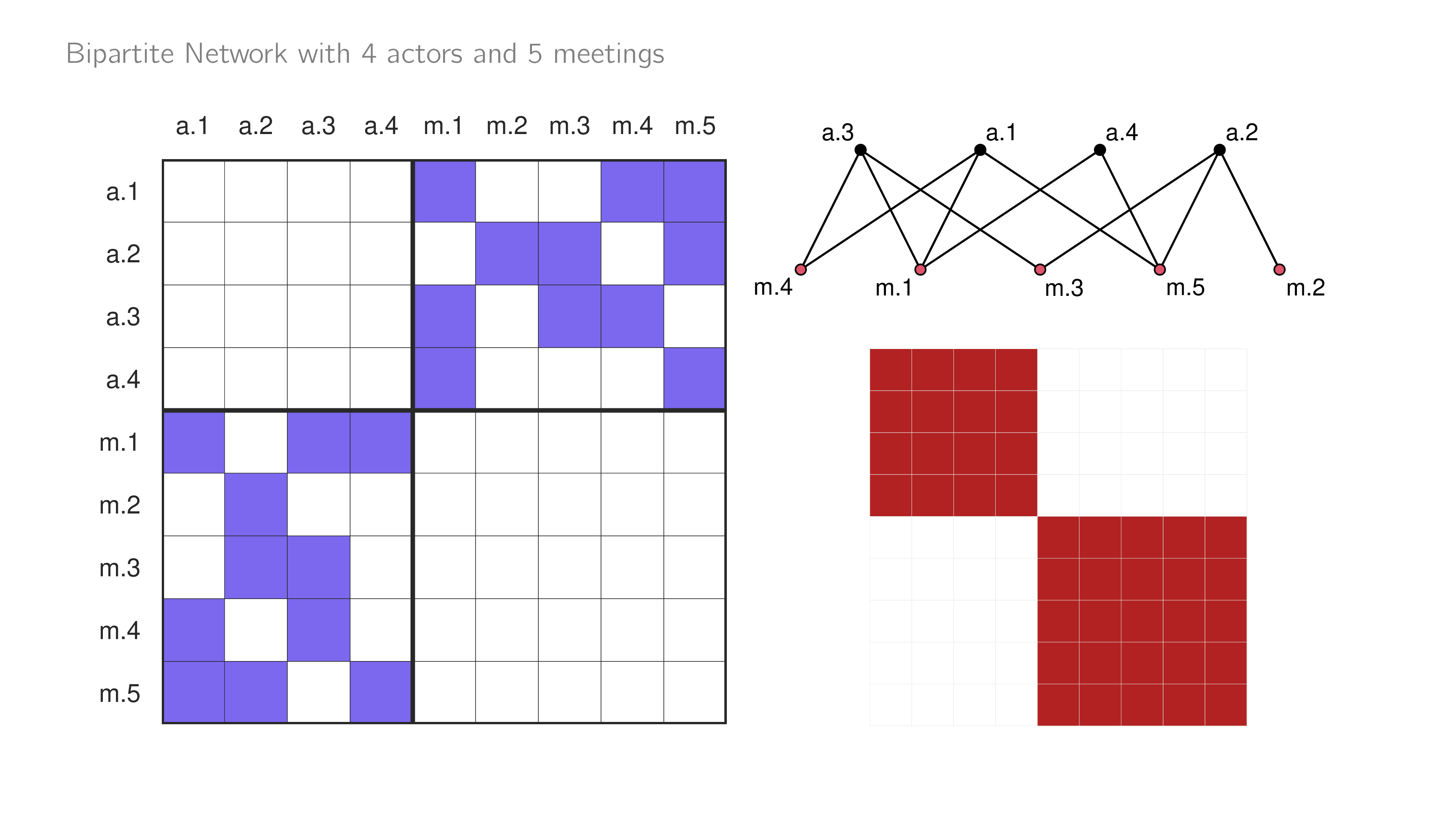
Constrained to no ties in the main diagonal blocks.

Bipartite networks are very common, and the ergm package has a lot of support for fitting these networks

(Kind of) Directed Acyclic Graphs

Directed acyclic graphs are directed graphs/networks that have no directed cycles

• In the social sciences, academic citation networks and judicial court citation networks are (kind of) directed acyclic graphs
• In academic publishing, working papers/preprints can lead to reciprocol citations
• In the US Supreme Court, cases decided within the same term can cite each other

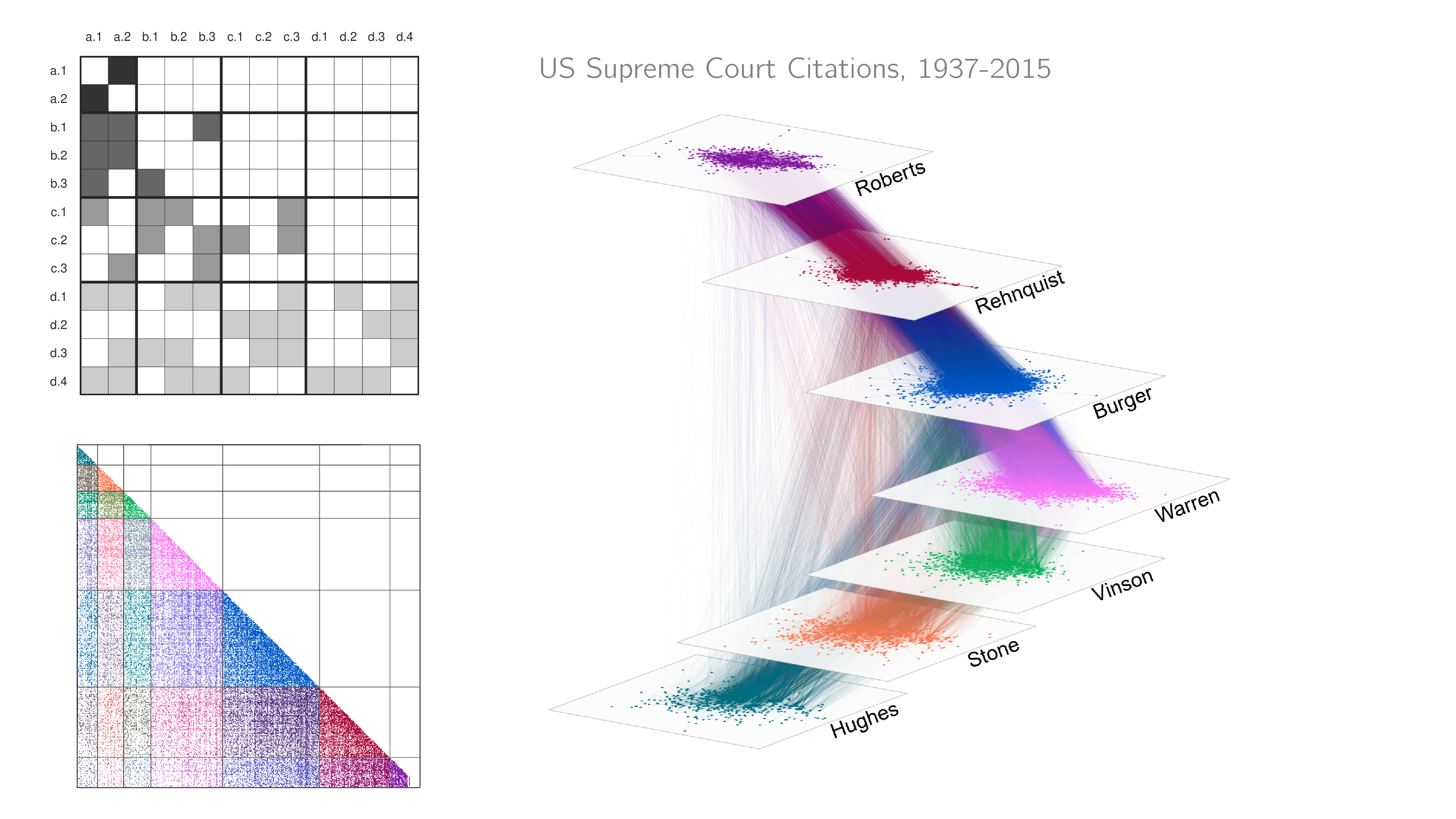
Constrained to no ties going back in order of publication unless they are within the same temporal period.

Resources:

• the cERGM package

Reference:

Schmid, CS et al. 2021. “Generative dynamics of supreme court citations: Analysis with a new statistical network model.” Political Analysis.

Specifying Relational Contexts

Relational contexts are conditions that systematically govern the probability of edge formation in a complex network. In the current discussion, they are researcher-specified.

• Extension of “conditional network effects” discussed in the introduction
• In different relational contexts, network effects are allowed to have different coefficients
• They can be understood as interaction terms
• They can be combined with constraints

Multilayer Networks

Networks that contain different types of relational contexts systematically organized into layers

• Flexible generalized framework that can account for many different types of network structures
• Network nodes are organized into layers, which represent different kinds of ties
• Temporal networks can be understood as multilayer networks where layers are temporal contexts

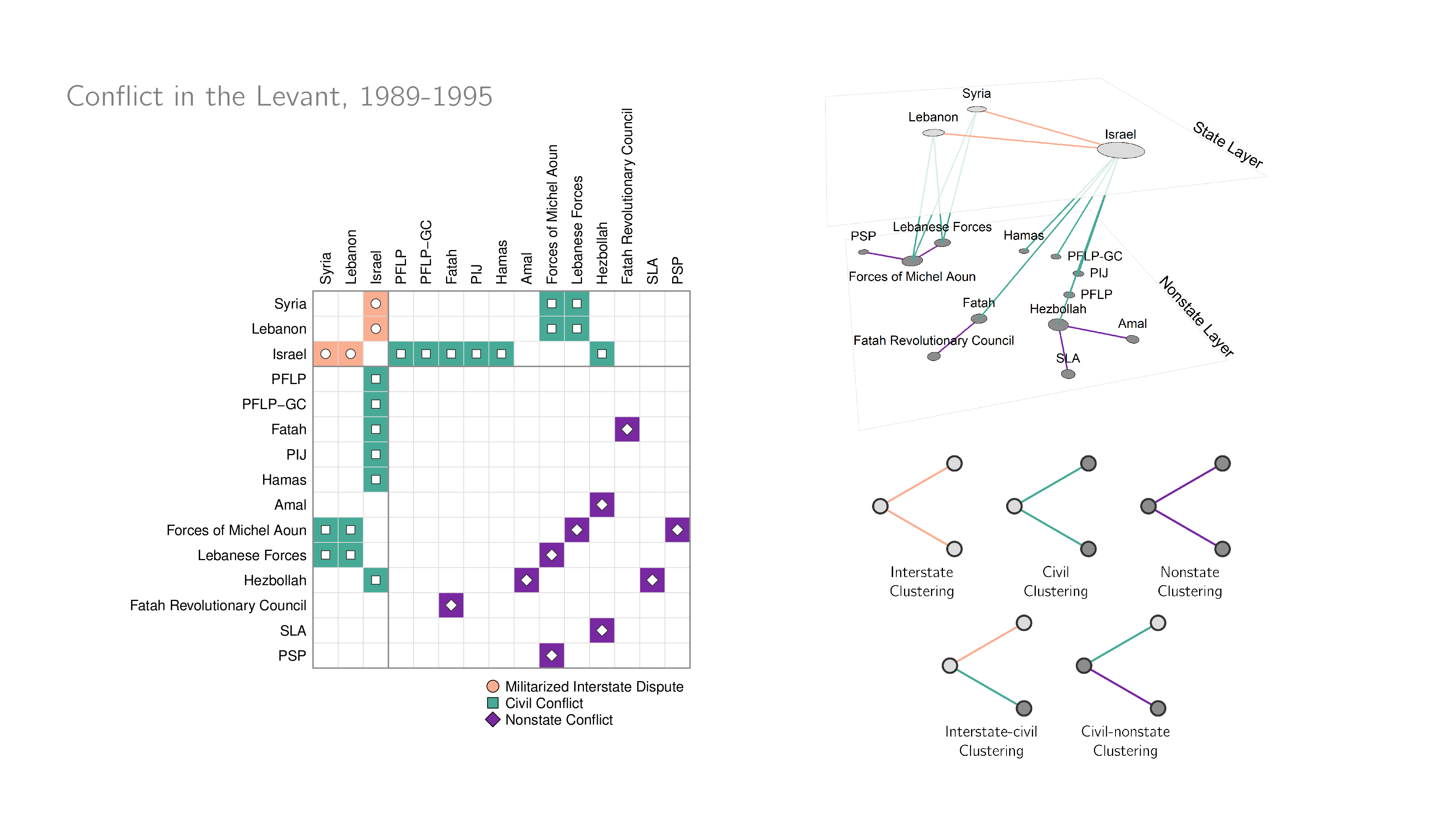
Three relational contexts with no constraints.

• By allowing for different kinds of ties to exist in a network, we can model different things with what are otherwise the same network configurations
• For example, the pile-on effect in conflicts are not likely to be the same across different combinations of actors

Resources:

• the multilayer.ergm package
• the MPNet application

Reference:

Chen, THY. 2021. “Statistical inference for multilayer networks in political science”. Political Science Research and Methods.

Wang, P et al. 2016 “Social selection models for multilevel networks.” Social Networks.

Temporal Networks

Temporal networks are networks where ties are time-period specific

• They are intuitive to understand as it, but in the context of network analysis, temporal networks can be understood as a special case of the multilayer networks
• The time periods of the ties are the relational contexts

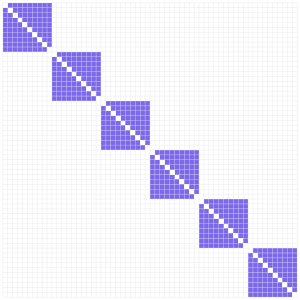
As many relational contexts as time periods, constrained to have no ties across periods.

• Only ties within each temporal layer (i.e. period) can exist while the others cells are held to no ties
• This formulation helps with more advanced ERGMs, but for temporal networks where each time period is relatively simple, existing formulations and packages perform very well already

Resources:

• the xergm package (specifically btergm)

Reference:

Leifeld, et al. 2018. “Temporal exponential random graph models with btergm: Estimation and bootstrap confidence intervals”. Journal of Statistical Software.